Aller au contenu

Programmation dynamique⚓︎

image

image

1. Retour sur la suite de Fibonacci⚓︎

1.1 Simple et inefficace⚓︎

Comme nous l'avons déjà vu ici, la suite de Fibonacci définie par :

  • \(F_0 = 0\)
  • \(F_1 = 1\)
  • \(\forall n \in \mathbb{N}, F_{n+2} = F_{n+1}+F_n\)

se programme récursivement par :

1
2
3
4
5
6
7
def fibo(n):
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibo(n-1) + fibo(n-2)

Ce code, d'une grande simplicité, est malheureusement très inefficace.

Exercice 1

Mesurer le temps de calcul de fibo(40).

Correction 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
import time

def fibo(n):
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibo(n-1) + fibo(n-2)

t0 = time.time()
fibo(40)
print(time.time() - t0)

Le temps de calcul est de plusieurs dizaines de secondes, sur une machine récente. C'est très mauvais !

En cause : la multitude des appels récursifs nous conduit à refaire des calculs déjà effectués.

Observons l'arbre d'appels de fibo(6) :

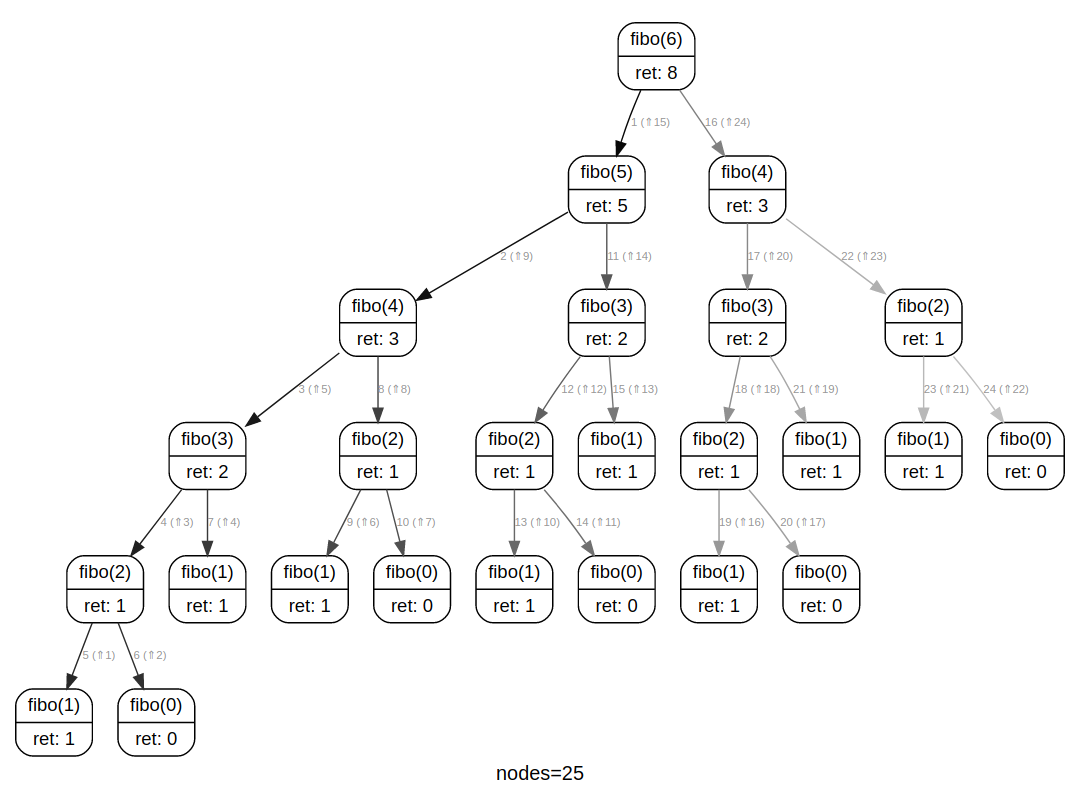
image

Le calcul de fibo(2) se retrouve ainsi 5 fois dans l'arbre.

Pour résoudre notre problème, nous l'avons divisé en problèmes plus petits, mais malheureusement pas indépendants : on dit que les problèmes se recouvrent, ce qui nous amène à refaire des choses déjà faites.

Dans l'algorithme de dichotomie, ou du tri-fusion, les problèmes étaient indépendants et ne se recouvraient pas : on ne refaisait jamais deux fois la même chose. Ce n'est pas le cas ici.

1.2 Se souvenir des belles choses des calculs : la mémoïsation⚓︎

Comment éviter de recalculer (par exemple) 5 fois fibo(2) ?

L'idée générale est de stocker le résultat de chaque calcul, par exemple dans un dictionnaire. Ainsi, à chaque demande de calcul :

  • Soit le calcul a déjà été effectué : on a donc juste à le lire dans le dictionnaire.
  • Soit le calcul n'a jamais été effectué : on l'effectue, et on stocke le résultat dans le dictionnaire.

Exercice 2

Compléter le code suivant :

1
2
3
4
5
6
dict_fibo = {0:0, 1:1}
def fibo(n):
    if n in dict_fibo:
        return ...
    dict_fibo[n] = ... + ...
    return ...
Correction 
1
2
3
4
5
6
dict_fibo = {0:0, 1:1}
def fibo(n):
    if n in dict_fibo:
        return dict_fibo[n]
    dict_fibo[n] = fibo(n-1) + fibo(n-2)
    return dict_fibo[n]

Exercice 3

Mesurer le temps de calcul de fibo(40) et comparer avec la mesure de l'exercice 1.

1.3 Quelques remarques⚓︎

1.3.1 ➡ Juste une brute-force plus efficace ?⚓︎

Notre technique de mémoïsation ne change pas vraiment la structure du programme : on continue de calculer toutes les valeurs intermédiaires, mais on ne les calcule qu'une seule fois.

image

1.3.2 ➡ Suppression de la variable globale⚓︎

Dans le code précédent, le dictionnaire dict_fibo est à l'extérieur de la fonction. Un dictionnaire étant un type mutable, sa modification à l'intérieur de la fonction ne pose pas de problème. Toutefois, ce genre de pratique est déconseillé : si par exemple on appelle 2 fois la fonction fibo, le dictionnaire n'est pas réinitialisé entre-temps (ce qui dans notre cas n'est pas problématique, mais cela pourrait l'être). Comment éviter cela ?

On peut utiliser une fonction englobante (appelée ici fibonacci ) :

1
2
3
4
5
6
7
8
def fibonacci(n):
    dict_fibo = {0:0, 1:1}
    def fibo(n):
        if n in dict_fibo:
            return dict_fibo[n]
        dict_fibo[n] = fibo(n-1) + fibo(n-2)
        return dict_fibo[n]
    return fibo(n)

>>> fibonacci(50)
12586269025

Remarquez la définition d'une fonction à l'intérieur d'une autre. Cela ne pose aucun problème, mais attention, cette fonction n'existe pas à l'extérieur de sa fonction englobante.

1.3.3 ➡ Mémoïsation automatique en Python ⭐ ⭐ ⭐⚓︎

La fonction lru_cache du module functools permet de mémoïser automatiquement une fonction récursive. Il suffit, juste avant d'écrire la fonction, de mettre la ligne @lru_cache (appelée décorateur). 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
import time
from functools import lru_cache

@lru_cache  #(1)
def fibo(n): #(2)
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibo(n-1) + fibo(n-2)

t0 = time.time()
fibo(35)
print(time.time() - t0)
  1. «décorateur» de la fonction
  2. Ceci est notre VIEILLE fonction fibo, extrêmement lente...

Essayez en commentant / décommentant la ligne 4... c'est magique !

1.4 De bas en haut⚓︎

La structure récursive naturelle de la suite de Fibonacci nous a conduit vers un programme qui calcule (ou plutôt appelle) les valeurs de haut en bas. (méthode top-down)

Et si on commençait par le bas ?

Si nous devions calculer mentalement le 6ème terme de la suite de Fibonacci, on commencerait par calculer le 3ème, puis le 4ème, puis le 5ème et enfin le 6ème.

Exercice 4

Compléter le code ci-dessous :

1
2
3
4
5
6
7
def fibo(n):
    dict_fibo = {}
    dict_fibo[0] = ...
    dict_fibo[1] = ...
    for k in range(..., ...):
        dict_fibo[k] = dict_fibo[...] + dict_fibo[...]
    return dict_fibo[...]
Correction 
1
2
3
4
5
6
7
def fibo(n):
    dict_fibo = {}
    dict_fibo[0] = 0
    dict_fibo[1] = 1
    for k in range(2, n+1):
        dict_fibo[k] = dict_fibo[k-1] + dict_fibo[k-2]
    return dict_fibo[n]

Cette méthode itérative part du bas pour aller vers le haut. On parle de méthode bottom-up. De manière plus générale, cette méthode est basée sur le fait de résoudre des problèmes de petite taille, puis de plus en plus gros, jusqu'au problème final.

1.5 Bilan des méthodes employées⚓︎

Principes de programmation dynamique ❤

  • Lors d'un calcul effectué de manière récursive, il peut arriver que de multiples appels récursifs soient identiques. Pour éviter de recalculer plusieurs fois la même chose, on peut stocker les résultats intermédiaires. On appelle cette technique la mémoïsation.
    Cette technique minimise le nombre d'opérations et accélère grandement l'exécution du programme. Le prix à payer est l'utilisation d'une structure de stockage des valeurs intermédiaires, et donc une augmentation de la mémoire utilisée par le programme.

  • Lors d'un calcul effectué de manière itérative, il est parfois plus simple de commencer par une «petite» version du problème pour progressivement remonter vers la solution du problème global.

2. Programmation dynamique et optimisation⚓︎

2.1 Optimisation d'une somme dans une pyramide⚓︎

Problème

Considérons la pyramide ci-dessous :

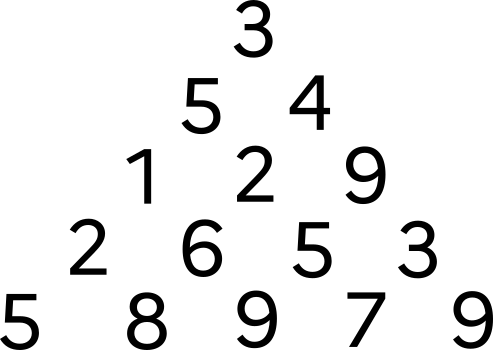
image

En partant du sommet et en descendant soit à gauche soit à droite, quel chemin donne la somme maximale en arrivant en bas ?

image

La suite : TP Pyramides

2.2 Problème du plus grand carré blanc⚓︎

Problème

Considérons l'image ci-dessous :

image

Quel est la taille du plus grand carré entièrement blanc qu'on puisse dessiner à l'intérieur de cette image ?

La suite : TP Plus Grand Carré Blanc

2.3 Optimisation du rendu de monnaie⚓︎

Problème

image

Étant donnés une liste de pièces pieces et une somme à rendre somme, peut-on calculer le nombre minimal de pièces pour réaliser cette somme ?

La suite : TP Rendu de monnaie