À la recherche du plus grand carré blanc

L'objectif est de trouver la taille du plus grand carré intégralement blanc que l'on peut dessiner dans l'image ci-dessous :

1. Prise en main

Préambule

Télécharger l'image, puis creér une variable img grâce au package PIL:

from PIL import Image
img = Image.open('pgcb.bmp')

On peut dès lors avoir accès à quelques informations :

>>> img.size
(600, 600)

L'image est donc de taille 600x600.

>>> img.getpixel((0, 0))
(255, 255, 255)
>>> img.getpixel((0, 358))
(0, 0, 0)

Le pixel de coordonnées (0, 0) est donc blanc, et le pixel (0, 358) est noir.

Exercice 1

Écrire une fonction est_noir qui prend en paramètre les coordonnées d'un pixel x et y et qui renvoie True si ce pixel est noir, False sinon.

Exemple :

>>> est_noir(0, 0)
False
>>> est_noir(0, 358)
True

Correction

from PIL import Image
img = Image.open('pgcb.bmp')

def est_noir(x, y):
    return img.getpixel((x,y)) == (0, 0, 0)

1.2 Recherche manuelle

Considérons le damier ci-dessous :

Pour chaque case, on va inscrire à l'intérieur la taille du plus grand carré blanc possible dont la case est le coin inférieur droit.

Par exemple :

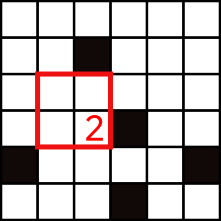
Sur une case noire, on écrira le nombre 0.

Exercice 2

Recopier le damier et compléter toutes les cases, en commençant en haut à gauche.

Correction

Imaginons maintenant la situation suivante, sur un autre damier que vous ne pouvez pas voir en intégralité :

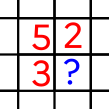
Exercice 3

Quelle est la valeur qu'il faut écrire à la place du point d'interrogation ?

Correction

Il faut écrire la valeur 3, qui est égale à 1 + le minimum des trois cases situées au Nord, Ouest et Nord-Ouest.

2. La fonction pgcb

pgcb -> plus grand carré blanc

2.1 Première écriture

On va écrire la fonction récursive pgcb, qui prend en paramètre un tuple (x,y) et qui renvoie la taille du plus grand carré blanc dont le pixel de coordonnées (x,y) est le coin inférieur droit.

Les cas de base seront :

• le pixel est noir : on renvoie 0
• le pixel est sur la ligne du haut ou la colonne de gauche : on renvoie 1

Pour le cas général, on s'inspirera de la partie précédente...

Exercice 4

Écrire le code de la fonction pgcb.

Exemples d'utilisation :

>>> pgcb(0,0)
1
>>> pgcb(3,2)
3
>>> pgcb(0,358)
0

Correction

def pgcb(x, y):
    if est_noir(x, y):
        return 0

    if x == 0 or y == 0:
        return 1

    return 1 + min(pgcb(x-1, y), pgcb(x, y-1), pgcb(x-1, y-1))

2.2 Amélioration de la fonction pgcb

Si on teste la fonction avec le pixel de coordonnées (300, 300), le code ne renvoie aucun résultat et semble parti dans des calculs interminables.

La structure récursive du code doit nous pousser à la méfiance : ne saurions-nous pas en train de lui demander de calculer plusieurs fois la même chose ?

La réponse est oui : si on ne regarde par exemple que les pixels diagonaux, l'appel pgcb(1, 1) aura lieu pour pgcb(2, 2), mais aussi pour pgcb(3, 3), pour pgcb(4, 4), pour pgcb(5, 5)... entre autres !

Pour éviter de refaire ces calculs, on va donc faire appel à la technique de mémoïsation.

Exercice 5

Écrire la fonction pgcb_memo, identique à la fonction pgcb mais qui mémoïse ses résultats. On pourra se servir d'une fonction englobante comme dans le cours sur Fibonacci.

Exemple :

>>> pgcb_memo(300,300)
21

Correction

def pgcb_memo(x, y):
    dict_memo = {}
    def pgcb(x, y):
        if est_noir(x, y):
            return 0
        if x == 0 or y == 0:
            return 1
        if (x, y) not in dict_memo:
            dict_memo[(x, y)] = 1 + min(pgcb(x-1, y), pgcb(x, y-1), pgcb(x-1, y-1))
        return dict_memo[(x, y)]
    return pgcb(x, y)

3. Recherche du plus grand carré

Maintenant que notre fonction est efficace, nous pouvons partir à la recherche du pixel de l'image d'où peut se construire le plus grand carré blanc.

Exercice 6

Écrire une fonction total_pgcb qui va parcourir tous les pixels de l'image et renvoyer la taille du plus grand carré blanc qu'on puisse y inscrire, ainsi que les coordonnées du pixel inférieur droit de ce carré.

Exemple :

>>> total_pgcb()
(51, (370, 461))

Dans la structure de votre code, penser à réutiliser le dictionnaire de mémoïsation...

Correction

def total_pgcb():
    dict_memo = {}
    def pgcb(x, y):
        if est_noir(x, y):
            return 0

        if x == 0 or y == 0:
            return 1

        if (x, y) not in dict_memo:
            dict_memo[(x, y)] = 1 + min(pgcb(x-1, y), pgcb(x, y-1), pgcb(x-1, y-1))
        return dict_memo[(x, y)]

    maxi = 0
    for x in range(600):
        for y in range(600):
            taille_pgcb = pgcb(x, y)
            if taille_pgcb > maxi:
                maxi = taille_pgcb
                best_pixel = (x, y)
    return maxi, best_pixel

On trouve donc :

>>> total_pgcb()
(51, (370, 461))

Voici la position de ce carré :

4. Bonus : méthode bottom-up

Exercice 7

En s'inspirant de la manière dont on a rempli manuellement les cases au 1.2, écrire une fonction pgcb_bottom_up.

Correction

def pgcb_bottom_up():
    memo = {}
    maxi = 0
    for x in range(600):
        for y in range(600):
            if est_noir(x, y):
                memo[(x,y)] = 0
            elif x == 0 or y == 0:
                memo[(x,y)] = 1
            else:
                memo[(x,y)] = 1 + min(memo[(x-1, y)] , memo[(x-1, y-1)] , memo[(x, y-1)])
            if memo[(x,y)] > maxi:
                maxi = memo[(x,y)]
                best = (x,y)
    return maxi, best