Aller au contenu

Exercices

Exercice 1

Exercice 3 du sujet 0 version A - 2024

Correction Q1.

image

Correction Q2.

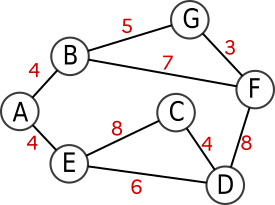
Le chemin le plus court est A-E-D (10 km).

Correction Q3.

La matrice d'adjacence de G1 est : \(\pmatrix{ 0 & 4 & 0 & 0 & 4 & 0 & 0 \\ 4 & 0 & 0 & 0 & 0 & 7 & 5 \\ 0 & 0 & 0 & 4 & 8 & 0 & 0 \\ 0 & 0 & 4 & 0 & 6 & 8 & 0 \\ 4 & 0 & 8 & 6 & 0 & 0 & 0 \\ 0 & 7 & 0 & 8 & 0 & 0 & 3 \\ 0 & 5 & 0 & 0 & 0 & 3 & 0 \\ }\)

Correction Q4. 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
G2 = {'A': ['B', 'C', 'H'],
      'B': ['A', 'I'],
      'C': ['A', 'D', 'E'],
      'D': ['C', 'E'],
      'E': ['C', 'D', 'G'],
      'F': ['G', 'I'],
      'G': ['E', 'F', 'H'],
      'H': ['A', 'G', 'I'],
      'I': ['B', 'F', 'H']
     }
Correction Q5.

Le parcours en largeur de ce graphe donne A-B-C-H-I-D-E-G-F.

Correction Q6.

La fonction cherche_itineraires s'appelle elle-même, elle est donc récursive.

Correction Q7.

La fonction cherche_itineraires sert à remplir la liste tab_itineraires (initialement vide) avec tous les chemins (uniques) partant de start et allant à end.

Code pour tester la Q8. 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
G2 = {'A': ['B', 'C', 'H'],
    'B': ['A', 'I'],
    'C': ['A', 'D', 'E'],
    'D': ['C', 'E'],
    'E': ['C', 'D', 'G'],
    'F': ['G', 'I'],
    'G': ['E', 'F', 'H'],
    'H': ['A', 'G', 'I'],
    'I': ['B', 'F', 'H']
    }

tab_itineraires = []
def cherche_itineraires(G, start, end, chaine=[]):
    chaine = chaine + [start]
    if start == end:
        return chaine
    for u in G[start]:
        if u not in chaine:
            nchemin = cherche_itineraires(G, u, end, chaine)
            if len(nchemin) != 0:
                tab_itineraires.append(nchemin)
    return []


def itineraires_court(G, dep, arr):
    cherche_itineraires(G, dep, arr)
    tab_court = ...
    mini = float('inf')
    for v in tab_itineraires:
        if len(v) <= ...:
            mini = ...
    for v in tab_itineraires:
        if len(v) == mini:
            tab_court.append(...)
    return tab_court
Correction Q8. 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
G2 = {'A': ['B', 'C', 'H'],
    'B': ['A', 'I'],
    'C': ['A', 'D', 'E'],
    'D': ['C', 'E'],
    'E': ['C', 'D', 'G'],
    'F': ['G', 'I'],
    'G': ['E', 'F', 'H'],
    'H': ['A', 'G', 'I'],
    'I': ['B', 'F', 'H']
    }

tab_itineraires = []
def cherche_itineraires(G, start, end, chaine=[]):
    chaine = chaine + [start]
    if start == end:
        return chaine
    for u in G[start]:
        if u not in chaine:
            nchemin = cherche_itineraires(G, u, end, chaine)
            if len(nchemin) != 0:
                tab_itineraires.append(nchemin)
    return []


def itineraires_court(G, dep, arr):
    cherche_itineraires(G, dep, arr)
    tab_court = []
    mini = float('inf')
    for v in tab_itineraires:
        if len(v) <= mini:
            mini = len(v)
    for v in tab_itineraires:
        if len(v) == mini:
            tab_court.append(v)
    return tab_court
Correction Q9.

Le problème vient de la variable globale tab_itineraires.

  • Après l'exécution de la commande itineraires_court(G2, 'A', 'E'), tab_itineraires contient tous les chemins de A à E.
  • Si le programme n'est pas re-exécuté, l'enchainement avec la commande itineraires_court(G2, 'A', 'F') va venir rajouter à la liste tab_itineraires tous les chemins de A à F.
  • Lors de la recherche du trajet minimum, les trajets testés seront donc à la fois les trajets de A à F mais aussi de A à E : on peut donc potentiellement avoir une réponse erronnée.

Pour éviter cela, on pourrait faire ceci (non demandé) :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def cherche_itineraires(G, start, end, chaine=[]):
    tab_itineraires = []
    def cherche(G, start, end, chaine=[]):
        chaine = chaine + [start]
        if start == end:
            return chaine
        for u in G[start]:
            if u not in chaine:
                nchemin = cherche(G, u, end, chaine)
                if len(nchemin) != 0:
                    tab_itineraires.append(nchemin)
        return []
    cherche(G, start, end, chaine=[])
    return tab_itineraires


def itineraires_court(G, dep, arr):
    tab_itineraires = cherche_itineraires(G, dep, arr)
    tab_court = []
    mini = float('inf')
    for v in tab_itineraires:
        if len(v) <= mini:
            mini = len(v)
    for v in tab_itineraires:
        if len(v) == mini:
            tab_court.append(v)
    return tab_court

Exercice 2

extrait de la BNS 2024

On considère dans cet exercice un graphe orienté représenté sous forme de listes d’adjacence.

On suppose que les sommets sont numérotés de 0 à n-1.

Par exemple, le graphe suivant :

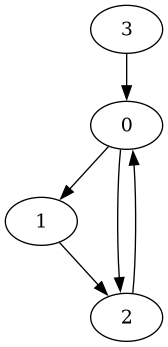
image

est représenté par la liste d’adjacence suivante :

adj = [[1, 2], [2], [0], [0]]

Écrire une fonction voisins_entrants(adj, x) qui prend en paramètre le graphe donné sous forme de liste d’adjacence et qui renvoie une liste contenant les voisins entrants du sommet x, c’est-à-dire les sommets y tels qu’il existe une arête de y vers x.

Exemples :

>>> voisins_entrants([[1, 2], [2], [0], [0]], 0)
[2, 3]
>>> voisins_entrants([[1, 2], [2], [0], [0]], 1)
[0]
Correction 
1
2
3
4
5
6
def voisins_entrants(adj, x):
    vois = []
    for i in range(len(adj)):
        if x in adj[i]:
            vois.append(i)
    return vois

Exercice 3

Dans cet exercice, on considère un graphe non orienté représenté sous forme de listes d’adjacence. On suppose que les sommets sont numérotés de 0 à n-1.

Ainsi, le graphe suivant:

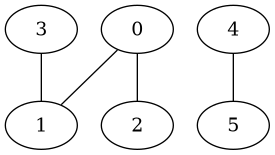
image

sera représenté par la liste d’adjacence suivante:

adj = [[1, 2], [0, 3], [0], [1], [5], [4]]

On souhaite déterminer les sommets accessibles depuis un sommet donné dans le graphe. Pour cela, on va procéder à un parcours en profondeur du graphe.

Compléter la fonction suivante.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
def parcours(adj, x, acc):
    '''Réalise un parcours en profondeur récursif
    du graphe donné par les listes d'adjacence adj 
    depuis le sommet x en accumulant les sommets
    rencontrés dans acc'''
    if x ...: 
        acc.append(x)
        for y in ...: 
            parcours(adj, ...) 

def accessibles(adj, x):
    '''Renvoie la liste des sommets accessibles dans le
    graphe donné par les listes d'adjacence adj depuis
    le sommet x.'''
    acc = []
    parcours(adj, ...) 
    return acc

Exemples : 

>>> accessibles([[1, 2], [0], [0, 3], [1], [5], [4]], 0)
[0, 1, 2, 3]
>>> accessibles([[1, 2], [0], [0, 3], [1], [5], [4]], 4)
[4, 5]

Correction 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
adj = [[1, 2], [0, 3], [0], [1], [5], [4]]

def parcours(adj, x, acc):
    '''Réalise un parcours en profondeur récursif
    du graphe donné par les listes d'adjacence adj
    depuis le sommet x en accumulant les sommets
    rencontrés dans acc'''
    if x not in acc:
        acc.append(x)
        for y in adj[x]:
            parcours(adj, y, acc)

def accessibles(adj, x):
    '''Renvoie la liste des sommets accessibles dans le
    graphe donné par les listes d'adjacence adj depuis
    le sommet x.'''
    acc = []
    parcours(adj, x, acc)
    return acc

Exercice 4

Exercice 2 du sujet Concours GEIPI 2024.

Codes du sujet :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
sentiers = [('Briana', 'La Concorde', 'Grand Palais', 100),
            ('Teddy', 'Grand Palais', 'Trocadéro', 550),
            ('Elaine', 'La Concorde', 'Trocadéro', 200),
            ('Lucie', 'Grand Palais', 'Champ de Mars', 512),
            ('Sydney', 'Trocadéro', 'Champ de Mars', 100)]

def creer_dico_arcs_sortants(sentiers):
    arcs_sortants = ...
    for (n, p1, p2, d) in sentiers:
        if ... not in arcs_sortants:
            arcs_sortants[ ... ] = []
        arcs_sortants[ ... ].append((p1, n, d))
        if ... not in ... :
            arcs_sortants[ ... ] = []
        arcs_sortants[ ... ].append( ... )
    return arcs_sortants

from math import inf # la constante inf représente (+ infini)
def plus_proche(a_visiter):
    min = ...
    proche = ''
    for (p, (poids, pred, sent)) in a_visiter.items():
        if ... <= ... :
            ( ... , ... ) = ( ... , ... )
    return ...

def meilleur_chemin(base, depart, arrivee):
    arcs = creer_dico_arcs_sortants(base)
    a_visiter = {p: (inf, '', '') for p in arcs.keys()}
    a_visiter[depart] = ...
    visites = ...
    while a_visiter != ... :
        # recherche du sommet suivant à visiter
        p = ...
        (dist,precedent,sentier) = a_visiter[p]
        # m-à-j des voisins de p restant à visiter
        for (suivant, n, d) in ... :
            if ... in a_visiter:
                (min,prec,sent) = ...
                poids = ... + dist
                if ... < ... :
                    a_visiter[suivant] = (..., ..., ...)
        # p passe des sommets à visiter aux sommets visités
        visites[p] = a_visiter[p]
        del a_visiter[p]
    affichage(visites, depart, arrivee)

def affichage(visites, depart, arrivee):
    pass
    (dist, depuis, nom) = visites[arrivee]
    pass
    if dist == inf:
        pass
        return
    pass
    if depart != arrivee:
        pass  
        pass
    pass
Correction Q1. 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
def creer_dico_arcs_sortants(sentiers):
    arcs_sortants = {}
    for (n, p1, p2, d) in sentiers:
        if p2 not in arcs_sortants:
            arcs_sortants[p2] = []
        arcs_sortants[p2].append((p1, n, d))
        if p1 not in arcs_sortants :
            arcs_sortants[p1] = []
        arcs_sortants[p1].append((p2, n, d))
    return arcs_sortants
Correction Q2. 
1
2
3
4
5
6
7
8
from math import inf # la constante inf représente (+ infini)
def plus_proche(a_visiter):
    min = inf
    proche = ''
    for (p, (poids, pred, sent)) in a_visiter.items():
        if poids <= min :
            ( min , proche ) = ( poids , p )
    return p
Correction Q3. 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
def meilleur_chemin(base, depart, arrivee):
    arcs = creer_dico_arcs_sortants(base)
    a_visiter = {p: (inf, '', '') for p in arcs.keys()}
    a_visiter[depart] = (0, '', '')
    visites = {}
    while a_visiter != {} :
        # recherche du sommet suivant à visiter
        p = plus_proche(a_visiter)
        (dist, precedent, sentier) = a_visiter[p]
        # m-à-j des voisins de p restant à visiter
        for (suivant, n, d) in arcs[p] :
            if suivant in a_visiter:
                (min, prec, sent) = a_visiter[suivant]
                poids = dist + d
                if poids < min :
                    a_visiter[suivant] = (poids, p, n)
        # p passe des sommets à visiter aux sommets visités
        visites[p] = a_visiter[p]
        del a_visiter[p]
    affichage(visites, depart, arrivee)
Correction Q4. 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def affichage(visites, depart, arrivee):
    pass
    (dist, depuis, nom) = visites[arrivee]
    pass
    if dist == inf:
        print('aucun chemin du point', depart, 'au point', arrivee)
        return
    pass
    if depart != arrivee:
        affichage(visites, depart, depuis)  
        print('en passant par le chemin', nom)
    print('étape au point', arrivee, '(distance', dist, ')')

Exercice 5

Exercice 2 du sujet Amérique du Nord J1 2024

Correction Q1.

image

Correction Q2. 
#                G, J, Y, E, N, M, A, L
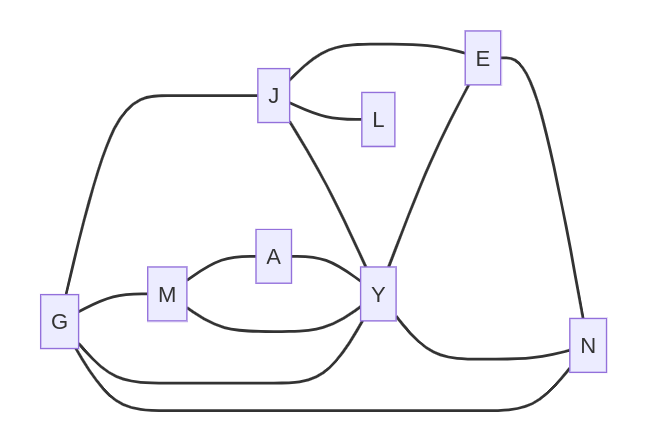
matrice_adj = [ [0, 1, 1, 0, 1, 1, 0, 0], #G
                [1, 0, 1, 1, 0, 0, 0, 1], #J
                [1, 1, 0, 1, 1, 1, 1, 0], #Y
                [0, 1, 1, 0, 1, 0, 0, 0], #E
                [1, 0, 1, 1, 0, 0, 0, 0], #N
                [1, 0, 1, 0, 0, 0, 1, 0], #M
                [0, 0, 1, 0, 0, 1, 0, 0], #A
                [0, 1, 0, 0, 0, 0, 0, 0]] #L
Correction Q3.
  • position(sommets, 'G') renvoie 0
  • position(sommets, 'Z') renvoie None
Correction Q4. 
1
2
3
4
5
6
7
8
def nb_amis(L, m, s):
    pos_s = position(L, s)
    if pos_s == None:
        return None
    amis = 0
    for i in range(len(m)):
        amis += m[pos_s][i]
    return amis
Correction Q5.

nb_amis(sommets, matrice_adj, 'G') renvoie 4.

Correction Q6.
  • c représente la clé.
  • v représente la valeur associée à cette clé.
Correction Q7. 
graphe = {
        'G' : ['J', 'Y', 'N', 'M'],
        'J': ['G', 'Y', 'E', 'L'],
        'Y': ['G', 'J', 'E', 'N', 'M', 'A'],
        'E': ['J', 'Y', 'N'],
        'N': ['G', 'Y', 'E'],
        'M': ['G', 'Y', 'A'],
        'A': ['Y', 'M'],
        'L': ['J']
        }
Correction Q8. 
def nb_amis(d, s):
    return len(d[s])
Correction Q9.

Le cercle d'amis de Lou est L J G Y E N.

⚠ Erreur d'énoncé sur la question 10.

Le code à compléter est celui-ci : 

1
2
3
4
5
6
7
visites = []
def parcours_en_profondeur(d, s):
    ...
    for v in d[s]:
        ...
            parcours_en_profondeur(d, v)
    ...

Correction Q10. 
1
2
3
4
5
6
7
visites = []
def parcours_en_profondeur(d, s):
    visites.append(s)
    for v in d[s]:
        if v not in visites:
            parcours_en_profondeur(d, v)
    return visites

Exercice 6 : l'algorithme de Dijkstra

L'algorithme de Dijkstra est un algorithme de recherche de plus court chemin dans un graphe, découvert en 1959 par le mathématicien et informaticien néerlandais Edsger Dijkstra.

Cet algorithme (plus exactement son optimisation A* que nous n'aborderons pas ici) est l'algorithme utilisé couramment par toutes les interfaces de recherche d'itinéraires (GPS des voitures, Itinéraires dans GoogleMaps, etc.)

Nous allons observer son fonctionnement sur un graphe en exemple, puis le programmer.

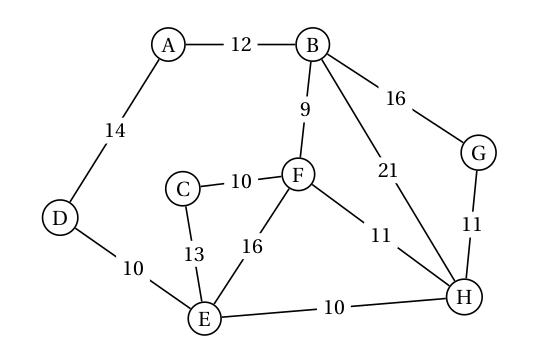
image

0. Fonctionnement⚓︎

1. Préambule⚓︎

À chaque étape il faut choisir le sommet qui est associé à la distance la plus petite. Nous allons pour cela devoir ordonner une liste par son deuxième élément.

Par exemple, vous voulons transformer la liste 

[["A", 3], ["B", 2], ["C", 8], ["D", 1]]

en 

[["D", 1], ["B", 2], ["A", 3], ["C", 8]]

Il faut pour cela procéder en 2 étapes.

➡ Créer une fonction deuxieme qui prend en paramètre un tableau lst de type List et qui renvoie le deuxième élément de lst.

Exemple d'utilisation 

>>> simpsons = ['Bart', 'Lisa', 'Maggie']
>>> deuxieme(simpsons)
'Lisa'

Correction 
def deuxieme(lst) :
    return lst[1]

Grâce à cette fonction deuxieme, nous allons utiliser la fonction sorted, qui prend en paramètre une liste à trier et une fonction de tri.

Exemple :

>>> mylist = [["A", 3], ["B", 2], ["C", 8]]
>>> mynewlist = sorted(mylist, key=deuxieme)
>>> mynewlist
[['B', 2], ['A', 3], ['C', 8]]
les fonctions lambda

Python permet en fait de faire cela de manière beaucoup plus rapide, avec les fonctions lambda, qui sont comme des fonctions créées à la volée sans avoir besoin de les nommer : 

>>> mylist = [["A", 3], ["B", 2], ["C", 8]]
>>> mynewlist = sorted(mylist, key=lambda x:x[1])
>>> mynewlist
[['B', 2], ['A', 3], ['C', 8]]

2. Algorithme de Dijkstra⚓︎

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
g = {
    'A': {'B': 12, 'D': 14},
    'B': {'A': 12, 'F': 9, 'G': 16},
    'C': {'E': 13, 'F': 10},
    'D': {'A': 14, 'E': 10},
    'E': {'D': 10, 'C': 13, 'F': 16, 'H': 10},
    'F': {'B': 9, 'C': 10, 'E': 16, 'H': 11},
    'G': {'B': 16, 'H': 11},
    'H': {'E': 10, 'F': 11, 'G': 11}
}


def deuxieme(lst):
    return ...

def classe_file(lst):
    return ...

def remonte_chemin(parent, start, end):
    s = end
    actuel = end
    while actuel != start:
        actuel = parent[actuel]
        s = actuel + s
    return s

def dijkstra(g, start, end):
    distance = {k:10**6 for k in g}
    distance[start] = 0
    parent = {}
    file = [(start, 0)]
    while file != []:
        file = ... #(1)
        actuel, dist = ... #(2)
        for voisin in ... : #(3)
            new_dist = ... + ... #(4)
            if new_dist < distance[voisin]:
                distance[voisin] = ... #(5)
                parent[voisin] = ... #(6)
                file.append((..., ...)) #(7)
    return remonte_chemin(parent, start, end), distance[end]
  1. On classe la file de sorte que le 1er élément soit le sommet ayant la plus petite distance.
  2. On sort de la liste ce premier élément, et on récupère le nom du sommet et sa distance associée.
  3. Les voisins du sommet actuel sont les clés du dictionnaire associé au sommet actuel.
  4. La nouvelle distance (potentielle) est la somme de la distance actuelle et de la distance entre actuel et voisin.
  5. On met à jour la distance.
  6. On met à jour le parent.
  7. On remet dans la file le sommet voisin ainsi que sa nouvelle distance associée.
Correction 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
g = {
    'A': {'B': 12, 'D': 14},
    'B': {'A': 12, 'F': 9, 'G': 16},
    'C': {'E': 13, 'F': 10},
    'D': {'A': 14, 'E': 10},
    'E': {'D': 10, 'C': 13, 'F': 16, 'H': 10},
    'F': {'B': 9, 'C': 10, 'E': 16, 'H': 11},
    'G': {'B': 16, 'H': 11},
    'H': {'E': 10, 'F': 11, 'G': 11}
}


def deuxieme(lst):
    return lst[1]

def classe_file(lst):
    return sorted(lst, key=deuxieme)

def remonte_chemin(parent, start, end):
    s = end
    actuel = end
    while actuel != start:
        actuel = parent[actuel]
        s = actuel + s
    return s

def dijkstra(g, start, end):
    distance = {k:10**6 for k in g}
    distance[start] = 0
    parent = {}
    file = [(start, 0)]
    while file != []:
        file = classe_file(file)
        actuel, dist = file.pop(0)
        for voisin in g[actuel].keys():
            new_dist = dist + g[actuel][voisin]
            if new_dist < distance[voisin]:
                distance[voisin] = new_dist
                parent[voisin] = actuel
                file.append((voisin, new_dist))
    return remonte_chemin(parent, start, end), distance[end]