Résolution d'un labyrinthe

1. Présentation du problème

Considérons le labyrinthe suivant :

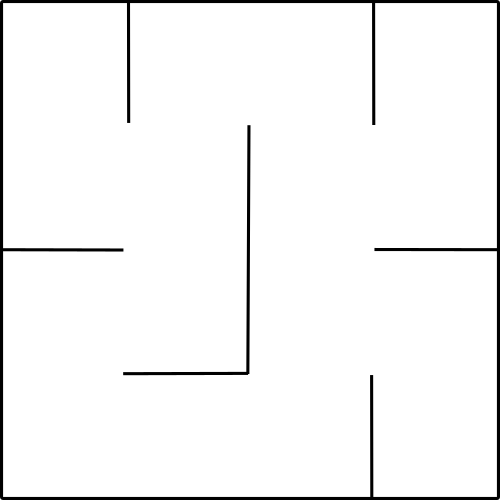
Affectons une lettre à chaque case de ce labyrinthe.

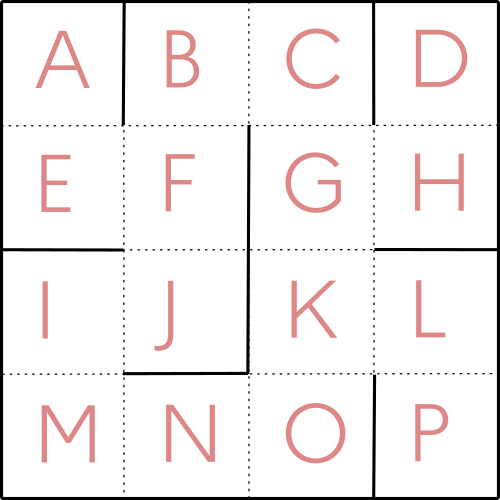
Notre objectif est de trouver comment aller de A en P.

2. Modélisation par un graphe

Exercice 1

Dessiner le graphe (dont les noeuds seront des lettres) qui modélise ce labyrinthe.

Proposer deux «formes» possibles pour ce graphe.

Correction

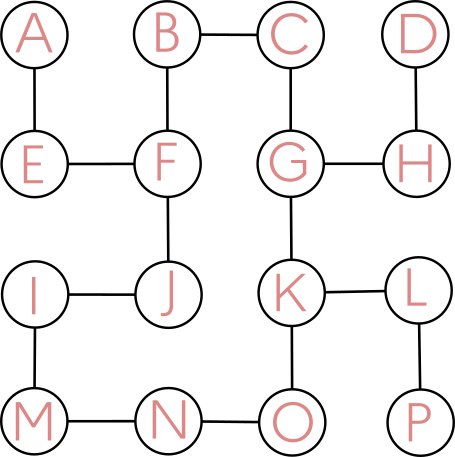
3. Implémentation du graphe en Python

Exercice 2

En utilisant la classe Graphe créée en cours, implémenter le graphe de ce labyrinthe.

Correction

class Graphe:
    def __init__(self, liste_sommets):
        self.liste_sommets = liste_sommets
        self.adjacents = {sommet : [] for sommet in liste_sommets}

    def ajoute_arete(self, sommetA, sommetB):
        self.adjacents[sommetA].append(sommetB)
        self.adjacents[sommetB].append(sommetA)

    def voisins(self, sommet):
        return self.adjacents[sommet]

    def sont_voisins(self, sommetA, sommetB):
        return sommetB in self.adjacents[sommetA]

g = Graphe(['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P'])
g.ajoute_arete('A', 'E')
g.ajoute_arete('E', 'F')
g.ajoute_arete('F', 'B')
g.ajoute_arete('B', 'C')
g.ajoute_arete('C', 'G')
g.ajoute_arete('G', 'H')
g.ajoute_arete('H', 'D')
g.ajoute_arete('G', 'K')
g.ajoute_arete('F', 'J')
g.ajoute_arete('J', 'I')
g.ajoute_arete('I', 'M')
g.ajoute_arete('M', 'N')
g.ajoute_arete('N', 'O')
g.ajoute_arete('O', 'K')
g.ajoute_arete('K', 'L')
g.ajoute_arete('L', 'P')

4. Recherche du plus court chemin

Exercice 3

En utilisant la fonction recherche_chemin du cours, établir le plus court chemin pour aller de A vers P dans ce labyrinthe.

Correction

def recherche_chemin(g, depart, arrivee):
    '''
    Parcours en largeur du graphe g en partant du sommet depart,
    qui s'arrête dès que le sommet arrivee est atteint.
    Renvoie alors le chemin du depart vers arrivee.
    '''
    traites = []
    decouverts = [depart]
    en_attente = [depart]
    parent = {}
    while en_attente != [] :
        sommet = en_attente.pop(0)
        voisins = g.voisins(sommet)
        for voisin in voisins:
            if voisin not in decouverts:
                decouverts.append(voisin)
                en_attente.append(voisin)
                parent[voisin] = sommet
                if voisin == arrivee:
                    return remonte_chemin(depart, arrivee, parent)
        traites.append(sommet)
    return 'non trouvé'  


def remonte_chemin(depart, arrivee, parent):
    sommet = arrivee
    chemin = arrivee
    while sommet != depart:
        sommet = parent[sommet]
        chemin = sommet + chemin
    return chemin

>>> recherche_chemin(g, 'A', 'P')
'AEFBCGKLP'

5. Conclusion

Sur un labyrinthe un peu plus imposant, voici l'illustration de notre méthode de résolution :

• le parcours en largeur part découvrir les cases dans toutes les directions.
• lorsque la case cherchée (ici, la rouge) est trouvée, on remonte à chaque case précédente grâce au dictionnaire parent, et ainsi le chemin de sortie du labyrinthe est généré.

Code de cette animation (en Pygame)

6. Annexe : et pourquoi pas en DFS ?

Les parcours BFS et DFS ont tous deux la propriété de parcourir la totalité du graphe (ils sont même conçus pour cela). Cela a permis au parcours BFS de nous fournir une solution au labyrinthe (dont on a démontré qu'elle était la plus courte).

Que penser de solution qui sera donnée par le DFS ?

6.1 Dans un labyrinthe parfait

Voici un code où la solution est d'abord recherchée par BFS (cases explorées en bleu clair, chemin trouvé marqué en bleu), puis en DFS (cases explorées en rose, chemin trouvé marqué en rouge).

anim_laby_DFSvsBFS_laby_parfait.py

Que remarquez-vous ???

6.2 Dans un labyrinthe non parfait

Changeons de code pour un labyrinthe dégénéré :

anim_laby_DFSvsBFS_laby_degenere.py

Que remarquez-vous ???

Explications

Notre labyrinthe conçu de manière aléatoire possède une propriété remarquable (dû son algorithme de construction) : chaque case peut être reliée à une autre par un chemin unique. On dit de ces labyrinthes qu'ils sont parfaits.

Donc, dans notre code du 6.1 (labyrinthe parfait), le DFS va lui aussi trouver le chemin le plus court... puisqu'il y en a qu'un seul ! De plus, la méthode d'exploration en profondeur va de plus rendre le DFS plus rapide que le BFS, quasiment tout le temps. Ce qui fait que pour un labyrinthe parfait, le DFS est plus intéressant que le BFS.

Mais si le labyrinthe n'est plus parfait (code du 6.2), le DFS va trouver une solution qui ne sera pas obligatoirement la meilleure... S'il y a plusieurs solutions possibles, absolument rien ne garantit que la première solution trouvée par le DFS (sur laquelle il s'arrêtera) sera la meilleure !