Aller au contenu

Exercices⚓︎

Exercice 1

Écrire une fonction récursive puissance qui prend en paramètres deux nombres x et n qui renvoie le nombre \(x^n\).

Correction 
1
2
3
4
5
def puissance(x, n):
    if n == 0:
        return 1
    else:
        return x * puissance(x, n-1)

Exercice 2 ❤

On rappelle que le PGCD (plus grand diviseur commun de deux nombres) vérifie la propriété suivante : si la division euclidienne de \(a\) par \(b\) s'écrit \(a = b \times q + r\), alors \(pgcd(a,b)=pgcd(b,r)\).

Cette propriété est à la base de l'algorithme d'Euclide

Exemple : \(pgcd(24,18)=pgcd(18,6)=pgcd(6,0)\), donc \(pgcd(24,18)=6\)

Écrire une fonction récursive pgcd qui prend en paramètres deux nombres a et b et qui renvoie leur PGCD.

Correction 
1
2
3
4
5
def pgcd(a, b):
    if b == 0:
        return a
    else:
        return pgcd(b, a % b)

Exercice 3

La conjecture de Syracuse (ou de Collatz) postule ceci :

Prenons un nombre \(n\) : si \(n\) est pair, on le divise par 2, sinon on le multiplie par 3 puis on ajoute 1. On recommence cette opération tant que possible. Au bout d'un certain temps, on finira toujours par tomber sur le nombre 1.

Q1. Écrire une fonction récursive syracuse qui prend en paramètres une entier n et qui écrivant tous les termes de la suite de Syracuse commençant à n , et s'arrêtant (on l'espère...) à la valeur 1.

Correction 
1
2
3
4
5
6
7
8
def syracuse(n):
    print(n)
    if n == 1:
        return None
    if n % 2 == 0:
        return syracuse(n // 2)
    else:
        return syracuse(3*n + 1)

Remarque : comme notre fonction syracuse ne renvoie pas de valeur numérique (elle ne fait qu'afficher une valeur), le return du test de parité est en fait inutile.

Mais le return du cas de base est lui primordial pour que le code s'arrête ! 

1
2
3
4
5
6
7
8
def syracuse(n):
    print(n)
    if n == 1:
        return None
    if n % 2 == 0:
        syracuse(n // 2)
    else:
        syracuse(3*n + 1)

Q2. On appelle «temps de vol» le nombre d'étapes nécessaires avant de retomber sur 1. Modifier la fonction précédente afin qu'elle affiche le temps de vol pour tout nombre n.

Correction 
1
2
3
4
5
6
7
8
9
def syracuse(n, t=0):
    print(n)
    if n == 1:
        print('temps de vol :', t)
        return None
    if n % 2 == 0:
        syracuse(n // 2, t+1)
    else:
        syracuse(3*n + 1, t+1)

Exercice 4

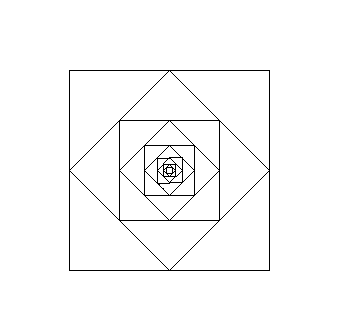
Reproduire le dessin suivant, à l'aide du module turtle.

turtle est un hommage au langage LOGO inventé par Seymour Papert au MIT à la fin des années 60.

Correction 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
from turtle import *
def carre(c):
    for k in range(4):
        forward(c)
        right(90)

def base(c):
    carre(c)
    forward(c/2)
    right(45)

def trace(c, n):
    if n == 0 :
        return None
    else :
        base(c)
        c = c/(2**0.5)
        trace(c, n-1)

trace(200, 5)

Exercice 5

Proposer une nouvelle fonction récursive puissance_mod qui prend en paramètres deux nombres x et n et qui renvoie le nombre \(x^n\). Pour optimiser la fonction déjà construite à l'exercice 1, utiliser le fait que :

  • si \(n\) est pair, \(a^n=(a \times a)^{n/2}\)
  • sinon \(a^n=a \times (a \times a)^{(n-1)/2}\)
Correction 
1
2
3
4
5
6
7
8
def puissance_mod(x, n):
    if n == 0 :
        return 1
    else :
        if n % 2 == 0:
            return puissance_mod(x*x, n//2)
        else :
            return x * puissance_mod(x*x, (n-1)//2)

Exercice 6

Écrire un algorithme récursif dicho_recursive qui prend en paramètres une liste triée (par ordre croissant) lst et une valeur val et qui renvoie un booléen indiquant la présence ou non de la valeur val dans une liste lst.

Exemple d'utilisation :

>>> lst = [2,4,5,5,7,9,11,15,16,18,19]
>>> dicho_recursive(lst, 16)
[2, 4, 5, 5, 7, 9, 11, 15, 16, 18, 19]
[9, 11, 15, 16, 18, 19]
[16, 18, 19]
[16]
True
>>> dicho_recursive(lst, 6)
[2, 4, 5, 5, 7, 9, 11, 15, 16, 18, 19]
[2, 4, 5, 5, 7]
[5, 5, 7]
[5, 7]
[5]
False

Aide :

Les techniques de slicing (hors-programme) permettent de couper une liste en deux : 

>>> lst = [10, 12, 15, 17, 18, 20, 22]
>>> lst[:3]
[10, 12, 15]
>>> lst[3:]
[17, 18, 20, 22]

Correction 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
def dicho_recursive(lst, val):
    print(lst) # pour voir la taille de la liste diminuer
    if len(lst) == 1:  #cas de base
        if lst[0] == val:
            return True
        else:
            return False
    else :              #cas récursif
        ind_milieu = len(lst)//2
        if lst[ind_milieu] > val:
            return recherche(lst[:ind_milieu], val)
        else:
            return recherche(lst[ind_milieu:], val)

Exercice 7

On considère le jeu des Tours de Hanoï. Le but est de faire passer toutes les assiettes de A vers C, sachant qu'une assiette ne peut être déposée que sur une assiette de diamètre inférieur.

Une version jouable en ligne peut être trouvée ici.

  1. S'entraîner et essayer d'établir une stratégie de victoire.
  2. Observer les images ci-dessous :

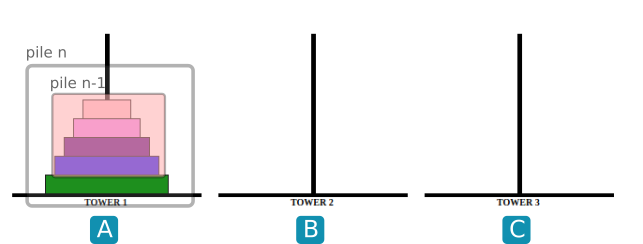
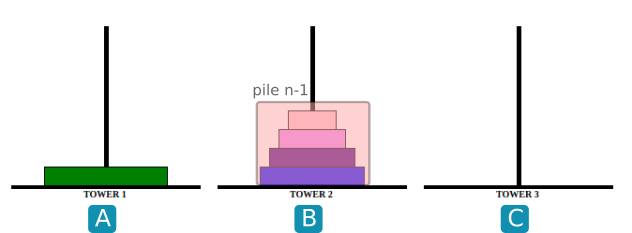
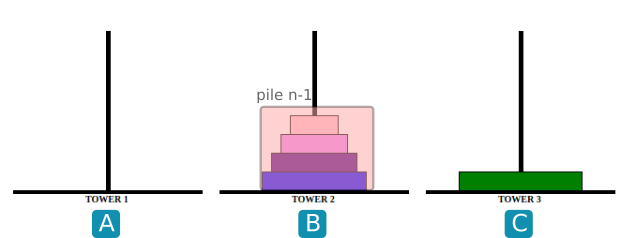
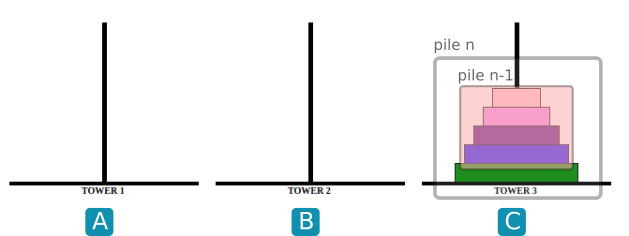
Écrire une fonction récursive hanoi(n, depart, inter, arrivee) qui donnera la suite d'instructions (sous la forme " A vers C") pour faire passer une pile de taille n de depart vers arrivee en prenant inter comme intermédiaire.

Correction 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
def hanoi(n, depart, inter, arrivee):
    ''' n : nombre d'assiettes dans la pile
    # depart : la pile de départ('A', 'B' ou 'C')
    # inter : la pile intermédaire('A', 'B' ou 'C')
    # arrivee : la pile d'arrivée ('A', 'B' ou 'C') '''

    if n == 1 :
        print(depart + ' vers ' + arrivee)
    else :
        hanoi(n-1, depart, arrivee, inter) 
        print(depart + ' vers ' + arrivee)
        hanoi(n-1, inter, depart, arrivee)

hanoi(5, 'A', 'B', 'C')

Exercice 8

Cet exercice a pour objectif le tracé du flocon de Von Koch.

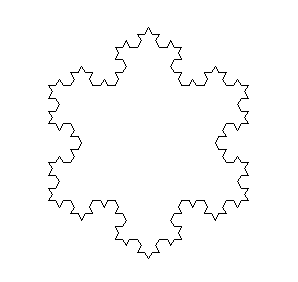
Les fractales

Ce flocon est une structure fractale, au même titre que le superbe ensemble de Mandelbrot, dont vous pouvez trouver une implémentation en Pygame ici.

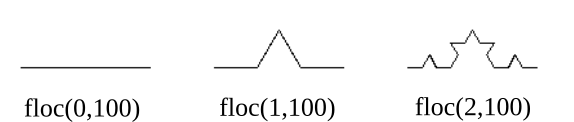
L'idée est de répéter de manière récursive la transformation ci-dessous : chaque segment de longueur l donne naissance à 4 segments de longueur l/3, en construisant une pointe de triangle équilatéral sur le deuxième tiers du segment.

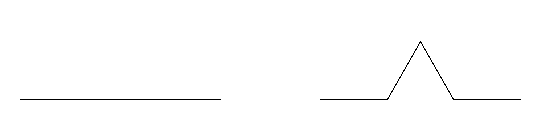
Q1. Créer une fonction récursive floc(n, l) qui trace à une «profondeur» n un segment de longueur l. Indications

  • l'instruction de tracé n'a lieu que quand n vaut 0.
  • l'étape n fait 4 appels successifs à l'étape n-1.

Q2. Créer une fonction triangle(n, l) qui trace le flocon complet.

Correction 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from turtle import *

def floc(n, l):
    if n == 0:
        forward(l)
    else:
        floc(n-1,l/3)
        left(60)
        floc(n-1,l/3)
        right(120)
        floc(n-1,l/3)
        left(60)
        floc(n-1,l/3)


speed(0)

def triangle(n,l):
    for _ in range(3):
        floc(n,l)
        right(120)

triangle(5,400)

Exercice 9

  1. Exercice 04.2 de la BNS 2022
  2. Application sur Capytale à retrouver ici

image

Correction 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def propager(grid, i, j, color):
    if grid[i,j].green == 0:
        return None # 

    grid[i,j].green = color

    # l'élément en haut fait partie de la composante
    if ((i-1) >= 0 and grid[i-1,j].green == 180):
        propager(grid, i-1, j, color)

    # l'élément en bas fait partie de la composante
    if ((i+1) < n and grid[i+1,j].green == 180):
        propager(grid, i+1, j, color)

    # l'élément à gauche fait partie de la composante
    if ((j-1) >= 0 and grid[i,j-1].green == 180):
        propager(grid, i, j-1, color)

    # l'élément à droite fait partie de la composante
    if ((j+1) < n and grid[i,j+1].green == 180): # 
        propager(grid, i, j+1, color)


grid = initgrid()
propager(grid,3,3,0)
grid.show()

Exercice 10

Exercice 4 du sujet Amérique du Nord J1 2022

Correction Q1.a.

Proposition 3

Correction Q1.b.

txt[0] vaut 'b'
txt[taille-1] vaut 'r'
interieur vaut 'onjou'

Correction Q2. 

1
2
3
def test_palindrome():
    assert palindrome('kayak') == True
    assert palindrome('canoe') == False
On teste les deux cas possibles.

Correction Q3. 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
def palindrome_imperatif(txt):
    if len(txt) < 2:
        return True
    i = 0
    j = len(txt)-1
    while i<j:
        if txt[i] != txt[j]:
            return False
        i += 1
        j -= 1
    return True
Correction Q4.a. 
1
2
3
4
5
6
def complementaire(txt):
    comp = {'A':'T', 'T':'A', 'G':'C', 'C':'G'}
    sol = ''
    for c in txt:
        sol += comp[c]
    return sol
Correction Q4.b

'GATCGTCTAGCA' n'est pas un palindrome donc 'GATCGT' n'est pas palindromique.

Correction Q4.c 
1
2
3
def est_palindromique(txt):
    txt_total = txt + complementaire(txt)
    return palindrome(txt_total)

Exercice 11

Exercice 1 du sujet Centres Étrangers J2 2022

Correction Q1.a.

f(5) affichera : `5 4 3 2 1 Partez!

Correction Q1.b.

On dit que cette fonction est récursive car elle s'appelle elle-même à l'intérieur de sa propre définition.

Correction Q2.a. 
1
2
3
4
5
def ajouter(s, liste):
    res = []
    for m in liste:
        res.append(s + m)
    return res
Correction Q2.b.

La commande renvoie : 

['ba', 'bb', 'bc']

Correction Q2.c.

La commande renvoie : 

['a']

Correction Q3.a.

Comme n vaut 0, on est dans le cas de base et donc la commande renvoie [""].

[""] n'est pas une liste vide, car elle contient un élément (une chaine de caractères vide). La liste vide est [].

Correction Q3.b.

produit('ab', 1) renvoie ['a', 'b'].

Correction Q3.c.

produit('ab', 2) renvoie ['aa', 'ab', 'ba', 'bb'].

Exercice 12

Exercice 1 du sujet Amérique du Nord J2 2024

Correction Q1 
1
2
3
4
def echange(tab, i, j):
    temp = tab[i]
    tab[i] = tab[j]
    tab[j] = temp
Correction Q2 
1
2
3
4
5
6
7
8
def triStooge(tab, i, j):
    if tab[i] > tab[j]:
        echange(tab, i, j)
    if j - i > 1:
        k = (j - i + 1) // 3
        triStooge(tab, i, j-k)
        triStooge(tab, i+k, j)
        triStooge(tab, i, j-k)
Correction Q3

Cet algorithme est récursif car aux lignes 6, 7 et 8, la fonction s'appelle elle-même.

Correction Q4

k vaut (5 - 0 + 1) // 3, donc k vaut 2.

Correction Q5
  • étape 1 : 3 appels
  • étape 2 : 9 appels
  • étape 3 : 27 appels

Il y a donc 39 appels au total.

Correction Q6
  • case 1 : triStooge(A,1,3)
  • case 2 : triStooge(A,2,3)
  • case 3 : triStooge(A,0,3)
Correction Q7

Correction probable, mais cette question est incompréhensible...

Appel Valeur de A avant l'appel Valeur de A après l'appel
triStooge(A,0,3) [5, 6, 4, 2] [2, 6, 4, 5]
triStooge(A,0,2) [2, 6, 4, 5] [2, 4, 6, 5]
triStooge(A,1,3) [2, 4, 6, 5] [2, 4, 5, 6]
triStooge(A,0,2) [2, 4, 5, 6] [2, 4, 5, 6]
Correction Q8

Nous connaissons (par exemple) le tri par sélection, dont l'ordre est en \(n^2\).

Comme \(2 < \frac{8}{3}\), on en déduit que le tri par sélection a un coût meilleur que le tri de Stooge.