Récursivité

1. Première approche

1.1. Définition

Fonction récursive

Une fonction est dite récursive lorsqu'elle fait appel à elle-même dans sa propre définition.

1.2 Un très mauvais exemple

C'est déjà une première chose à comprendre : un programme peut être appelé par lui-même, à l'intérieur de sa propre définition.

def prems():
    print("un très mauvais exemple")
    prems()

Si on appelle cette fonction, par la commande :

>>> prems()

La sortie en console sera celle-ci :

un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
un très mauvais exemple
...

Évidemment, comme prévu, ce programme ne s'arrête pas. Nous sommes obligés de l'arrêter manuellement. Nous sommes (volontairement) tombés dans un piège qui sera systématiquement présent lors d'une programmation récursive : le piège de la boucle infinie.

1.3 La mauvaise réputation

Dans la culture informatique, la récursivité est (trop) souvent abordée par le biais de l'auto-référence, le puits sans fin de la boucle infinie.

On trouve d'ailleurs fréquemment cette définition de la récursivité :

Fonction récursive : fonction qui fait appel à la récursivité. Voir fonction récursive.

Google fait aussi (dans toutes les langues) la même blague lors d'une recherche sur le terme «récursivité» :

Les acronymes récursifs sont aussi très fréquents... et véhiculent avec eux le même piège : une fonction récursive ne serait jamais vraiment définie (c'est faux, nous le verrons)

Par exemple :

• GNU (dans GNU/Linux) signifie GNU is Not Unix. On ne sait jamais vraiment ce que signifie GNU...
• PHP (le langage serveur) sigifie PHP: Hypertext Preprocessor
• VISA (les cartes bancaires) signifie VISA International Service Association.

2. La récursivité, ça marche !

Disons-le clairement : au-delà de la blague pour initiés (dont vous faites partie maintenant) la récursivité ne DOIT PAS être associée à une auto-référence vertigineuse : c'est en algorithmique une méthode (parfois) très efficace, à condition de respecter une règle cruciale : l'existence d'un CAS DE BASE .

Ce «cas de base» sera aussi appelé «condition d'arrêt», puisque la très grande majorité des algorithmes récursifs peuvent être perçus comme des escaliers qu'on descend marche par marche, jusqu'au sol qui assure notre arrêt.

2.1 La récursivité en BD

Observez bien la descente puis la remontée de notre vendeur de livre. Le cas de base est ici l'étage 0. Il empêche une descente infinie.

Nous coderons bientôt la fonction donnant le prix du livre en fonction de l'étage.

Pour l'instant, découvrons enfin à quoi ressemble une fonction récursive «bien écrite» :

2.2 Enfin un bon exemple

Exemple fondateur n°1

def mystere(n):
    if n == 0 :
        return 0
    else : 
        return n + mystere(n-1)

Trois choses sont essentielles et doivent se retrouver dans tout programme récursif :

• lignes 2 et 3 : le cas de base (si n vaut 0 on renvoie vraiment une valeur, en l'occurence 0)
• ligne 5 : l'appel récursif
• ligne 5 : la décrémentation du paramètre d'appel

Utilisation de la fonction mystere

>>> mystere(0)
0
>>> mystere(4)
10

Analyse grâce à PythonTutor

Que se passe-t-il lorsqu'on appelle mystere(4) ?

\[\begin{align} \rm{mystere(4)} &= 4+ \rm{mystere(3)}\\ &= 4+ (3+\rm{mystere(2)}) \\ &= 4+ (3+(2+\rm{mystere(1)} )) \\ &= 4+ (3+(2+(1+\rm{mystere(0)} ))) \\ &= 4+ (3+(2+(1+0 ))) \\ \end{align}\]

On voit que l'existence du cas de base pour \(n=0\) est primordiale pour éviter la récursion infinie.

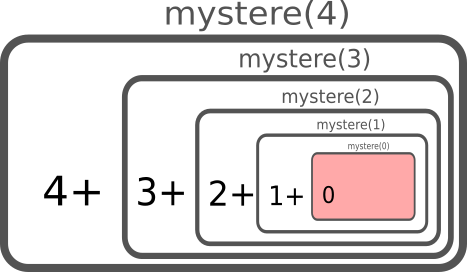
Cette fonction mystere(n) calcule donc la somme des entiers positifs inférieurs ou égaux à \(n\).

Remarque historique

mystere(100) est égal à 5050. Une anecdote raconte que Carl Friedrich Gauss trouva cette valeur de 5050 en quelques secondes, devant son instituteur ébahi.
Il venait pour cela d'inventer la formule : \(1+2+3+\dots+n=\frac{n(n+1)}{2}\)

Ici, \(1+2+3+\dots+100=\frac{100\times 101}{2}=50 \times 101=5050\)

Exercice 1

Coder la fonction prix de la BD présentée plus haut, qui prend en paramètre un entier positif etage et qui renvoie le prix de vente de la BD.

Correction

def prix(etage):
    if etage == 0:
        return 3
    else:
        return 2 * prix(etage - 1)

Exercice 2

On considère la fonction factorielle (notée \(n!\) en mathématiques), qui prend en paramètre un entier positif n et qui calcule le produit de \(n\) et de tous les entiers positifs qui lui sont inférieurs:

\[ n! = n \times (n-1) \times (n-2) \times \dots \times 3 \times 2 \times 1\]

Exemple : \(5!=5\times4\times3\times2\times1=120\)

Par convention, \(1!=1\)

Q1. Programmer de manière impérative (dite aussi manière itérative ou manière classique) la fonction factorielle. On l'appelera fact_imp.

Q2. Programmer de façon récursive la fonction factorielle. On l'appelera fact_rec.

Quelle paradigme de programmation vous a semblé le plus naturel ?

3. Le mécanisme interne de la récursivité

3.1 Notion de pile

Lors d'un appel à une fonction récursive, le processeur utilise une structure de pile pour stocker les contextes d'exécution de chaque appel. Dans la notion de pile (voir ici), seule l'instruction «en haut de la pile» peut être traitée et enlevée (on dit «dépilée»).

La pile d'appels de notre fonction mystere(5) peut donc être schématisée comme ceci :

3.2 Limitation de la taille de la pile

Nous venons de voir que notre appel à mystere(5) générait une pile de hauteur 6 (on parlera plutôt de profondeur 6). Cette profondeur est-elle limitée ?

mystere(2962)

---------------------------------------------------------------------------

RecursionError                            Traceback (most recent call last)

<ipython-input-32-a97c4dde4ef8> in <module>
----> 1 mystere(2962)


<ipython-input-1-386660a434f2> in mystere(n)
      3         return 0
      4     else :
----> 5         return n + mystere(n-1)


... last 1 frames repeated, from the frame below ...


<ipython-input-1-386660a434f2> in mystere(n)
      3         return 0
      4     else :
----> 5         return n + mystere(n-1)


RecursionError: maximum recursion depth exceeded in comparison

Vous venons de provoquer un «débordement de pile», le célèbre stack overflow.

De manière générale, les programmes récursifs sont souvent susceptibles de générer un trop grand nombre d'appels à eux-mêmes. Il est parfois possible de les optimiser, comme nous le verrons dans le cours concernant la programmation dynamique.

Nous reparlerons aussi de récursivité lorsque nous l'inscrirons dans un paradigme plus global de programmation, qui est « diviser pour régner » (en anglais divide and conquer).

4. Exemples de récursivité double

4.1 La suite de Fibonacci

Considérons la suite numérique ainsi définie :

• \(F_0 = 0\)
• \(F_1 = 1\)
• \(\forall n \in \mathbb{N}, F_{n+2} = F_{n+1}+F_n\)

On a donc \(F_2=0+1=1, F_3=F_2+F_1=1+1=2, F_4=F_3+F_2=2+1=3, F_5=F_4+F_3=3+2=5\) ...

Exercice 3

Implémenter de façon récursive la suite de Fibonacci.

Observation de la pile d'exécution

Appelons F(n) la fonction calculant de manière récursive le n-ième terme de la suite. Observons en détail la pile d'exécution lors du calcul de F(4).

Analyse grâce à PythonTutor

On s'aperçoit notamment que :

• les appels récursifs ne sont PAS simultanés (rappelons que la simultanéité n'existe pas en informatique). On pourrait s'imaginer que la relation \(F_4=F_3+F_2\) allait déclencher deux «fils» récursifs calculant respectivement \(F_3\) et \(F_2\). Il n'en est rien, on va jusqu'au bout du calcul de \(F_3\) avant de s'intéresser à \(F_2\).
• conséquence de la remarque précédente : le calcul de \(F_2\) s'effectue 2 fois. Une amélioration future (appelée mémoïsation, voir le cours de programmation dynamique) sera de conserver cette valeur de \(F_2\) afin d'améliorer les calculs.

Le module rcviz permet d'observer l'arbre des appels récursifs : voir cette activité Capytale

On peut y construire par exemple l'arbre d'appel de fibo(6) :

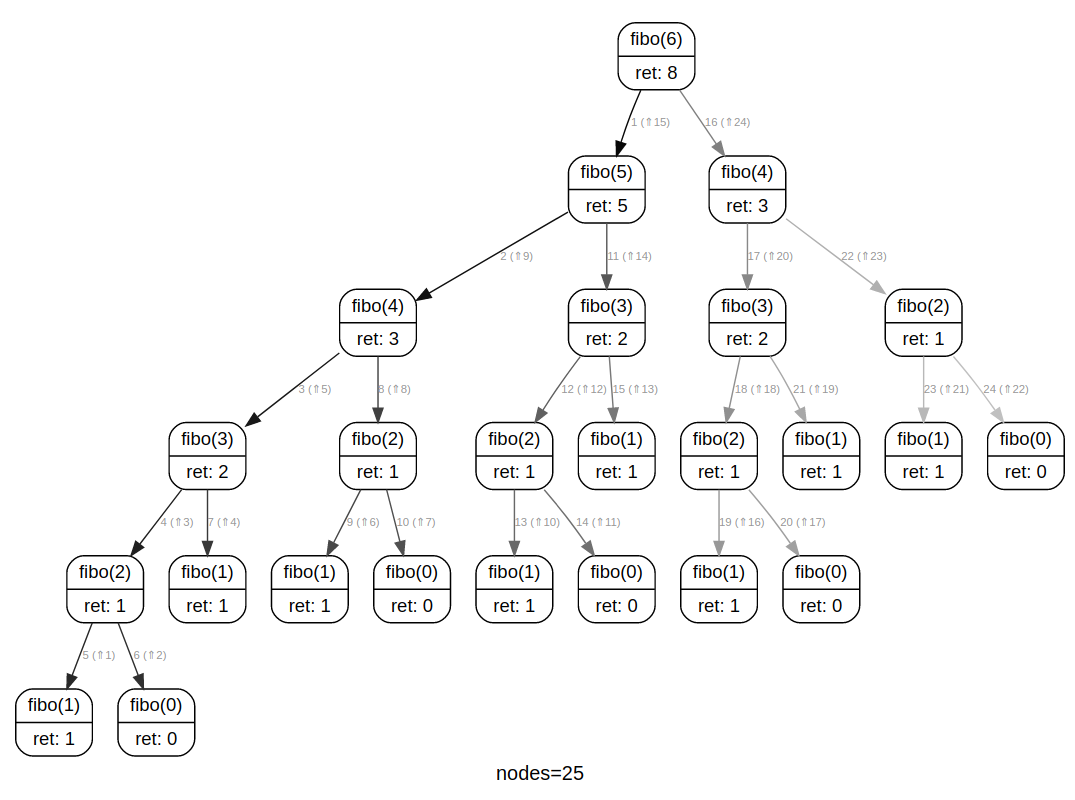
On y remarque (par exemple) que fibo(2) est calculé 5 fois...

4.2 Comparaison des performances

Exercice 4

Écrire une fonction fibo_imperatif(n) qui calcule de façon directe (impérative) le n-ième terme de la suite de Fibonacci. On pourra par exemple utiliser un dictionnaire.

Correction

def fibo_imperatif(n):
    f = {}
    f[0] = 0
    f[1] = 1
    for k in range(2, n+1):
        f[k] = f[k-1] + f[k-2]
    return f[n]

Construisons une fonction comparaison qui affichera le temps de calcul pour chacune des deux fonctions fibo_imperatif et fibo_recursif :

import time

def fibo_imperatif(n):
    f = {}
    f[0] = 0
    f[1] = 1
    for k in range(2, n+1):
        f[k] = f[k-1] + f[k-2]
    return f[n]

def fibo_recursif(n):
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibo_recursif(n-1) + fibo_recursif(n-2)


def comparaison(n):
    t0 = time.time()
    fibo_imperatif(n)
    print("algo impératif : ", time.time() - t0)
    t0 = time.time()
    fibo_recursif(n)
    print("algo récursif : ", time.time() - t0)

Résultats

>>> comparaison(10)
algo impératif :  6.9141387939453125e-06
algo récursif :  1.7642974853515625e-05
>>> comparaison(20)
algo impératif :  7.62939453125e-06
algo récursif :  0.0021445751190185547
>>> comparaison(30)
algo impératif :  1.8596649169921875e-05
algo récursif :  0.25478553771972656
>>> comparaison(40)
algo impératif :  1.1920928955078125e-05
algo récursif :  31.332343339920044

La fonction récursive apparait donc beaucoup, beaucoup plus lente que l'impérative (ici d'un facteur 100 pour toute augmentation de 10 du paramètre n.)

Attention : cette comparaison des vitesses d'éxécution peut être critiquée car les deux programmes n'ont pas la même complexité. Nous étudierons la complexité au moment des algorithmes de tri. La complexité des fonctions récursives n'est pas au programme de NSI.

Peut-on résumer la récursivité à une méthode élégante mais inefficace ? Ce serait réducteur : l'efficacité c'est aussi avoir un code lisible et intuitif. Nous en reparlerons lors du parcours des arbres et des graphes. (cf aussi l'exercice sur les Tours de Hanoï)

5. Annexe : dessins récursifs grâce au module turtle

Le module turtle permet de faire des tracés basiques. Mais dès l'instant où on met de la récursivité dans le code, les résultats peuvent devenir très surprenants, et aboutir à des structures fractales.

from turtle import *

ang = 40

def trace(n,l):
    if n == 0 :
        return None
    else :
        forward(l)
        left(ang)
        trace(n-1, 0.7*l)
        right(2*ang)
        trace(n-1, 0.7*l)
        left(ang)
        forward(-l)


penup()        
goto(0,-80)
pendown()
left(90)
speed(0)

trace(5,100)