Les opérateurs booléens⚓︎
1. Repères historiques⚓︎
En 1847, le britannique George BOOLE inventa un formalisme permettant d'écrire des raisonnements logiques : l'algèbre de Boole. La notion même d'informatique n'existait pas à l'époque, même si les calculs étaient déjà automatisés (penser à la Pascaline de 1642).
Bien plus tard, en 1938, les travaux de l'américain Claude SHANNON prouva que des circuits électriques peuvent résoudre tous les problèmes que l'algèbre de Boole peut elle-même résoudre. Pendant la deuxième guerre mondiale, les travaux d'Alan TURING puis de John VON NEUMANN poseront définitivement les bases de l'informatique moderne.
2. Algèbre de Boole⚓︎
L'algèbre de Boole définit des opérations dans un ensemble qui ne contient que deux éléments notés 0 et 1, ou bien FAUX et VRAI ,ou encore False et True (en Python)
Les opérations fondamentales sont :
- la conjonction ("ET")
- la disjonction ("OU")
- la négation ("NON").
Dans toute la suite, x et y désigneront des Booléens (éléments d'une
algèbre de Boole) quelconques, F désignera FAUX et V désignera VRAI.
2.1 Conjonction (AND)⚓︎
- symbole usuel : & (appelé esperluette en français et ampersand en anglais)
- français : ET
- anglais (et Python) :
and - notation logique : \(\wedge\)
- notation mathématique :
.
C'est l'opération définie par:
x & F = Fx & V = x
Puisque l'algèbre de Boole ne contient que deux éléments, on peut étudier tous les cas possibles et les regrouper dans un tableau appelé table de vérité:
Table de vérité de AND 
x |
y |
x & y |
|---|---|---|
| F | F | F |
| F | V | F |
| V | F | F |
| V | V | V |
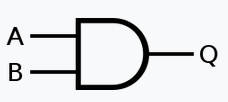
On représente souvent les opérateurs booléens à l'aide de portes logiques:
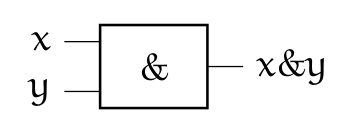
Notation usuelle en électronique : \(Q=A \wedge B\)
Exemples en Python⚓︎
>>> n = 20
>>> (n % 10 == 0) and (n % 7 == 0)
False
>>> (n % 4 == 0) and (n % 5 == 0)
True
L'évaluation paresseuse⚓︎
Pouvez-vous prévoir le résultat du code ci-dessous ?
>>> (n % 4 == 0) and (n % 0 == 0)
---------------------------------------------------------------------------
ZeroDivisionError Traceback (most recent call last)
<ipython-input-3-d8a98dcba9be> in <module>
----> 1 (n % 4 == 0) and (n % 0 == 0)
ZeroDivisionError: integer division or modulo by zero
Évidemment, la division par 0 provoque une erreur.
Mais observez maintenant ce code :
>>> (n % 7 == 0) and (n % 0 == 0)
False
On appelle évaluation paresseuse le fait que l'interpréteur Python s'arrête dès que sa décision est prise : comme le premier booléen vaut False et que la conjonction and est appelée, il n'est pas nécessaire d'évaluer le deuxième booléen.
2.2 Disjonction (OR)⚓︎
- symbole usuel : | appelé pipe en anglais
- français : OU
- anglais (et Python) :
or - notation logique : \(\vee\)
- notation mathématique : \(+\)
C'est l'opération définie par:
C'est l'opération définie par:
x | V = Vx | F = x
On en déduit la table suivante:
Table de vérité de OR
x |
y |
x or y |
|---|---|---|
| F | F | F |
| F | V | V |
| V | F | V |
| V | V | V |
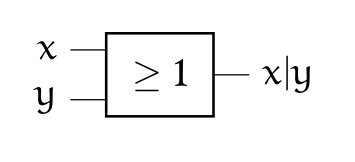
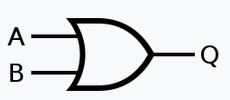
Notation usuelle en électronique : \(Q=A \vee B\)
Exemples en Python⚓︎
>>> n = 20
>>> (n % 10 == 0) or (n % 7 == 0)
True
>>> (n % 4 == 0) or (n % 5 == 0)
True
>>> (n % 7 == 0) or (n % 3 == 0)
False
L'évaluation paresseuse (retour)⚓︎
Pouvez-vous prévoir le résultat du code ci-dessous ?
>>> (n % 5 == 0) or (n % 0 == 0)
2.3 Négation (NOT)⚓︎
- symbole usuel : ~
- français : NON
- anglais (et Python) :
not - notation logique : \(\neg\)
- notation mathématique : \(\overline{x}\)
C'est l'opération définie par:
~V = F~F = V
On en déduit la table suivante:
Table de vérité de NOT
x |
~x |
|---|---|
| F | V |
| V | F |
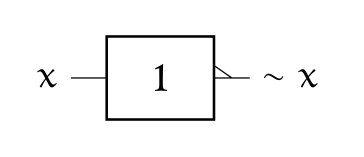
Notation usuelle en électronique : \(Q=\neg A\)
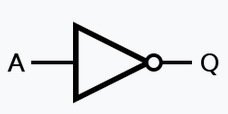
Exemples en Python⚓︎
>>> n = 20
>>> not(n % 10 == 0)
False
2.4 Exercice⚓︎
Exercice 1
Comprendre ce mème :
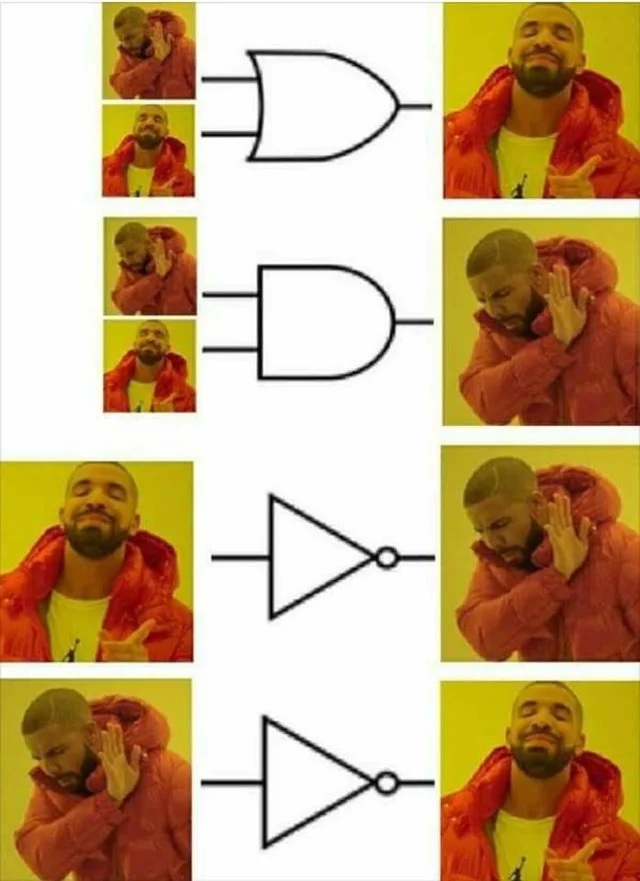
2.5 Exercice⚓︎
Exercice 2
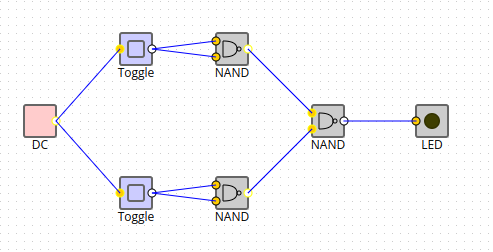
Ouvrir le simulateur de circuits et créer pour chaque opération AND, OR, NOT un circuit électrique illustrant ses propriétés.
Exemple (inintéressant) de circuit :
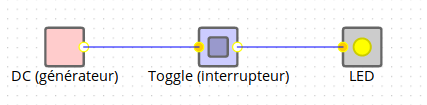
3. Fonctions composées⚓︎
3.1 Disjonction exclusive XOR⚓︎
(en français OU EXCLUSIF)
x ^ y = (x & ~y) | (~x & y)
Table de vérité de XOR
x |
y |
x ^ y |
|---|---|---|
| F | F | F |
| F | V | V |
| V | F | V |
| V | V | F |
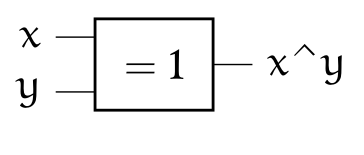
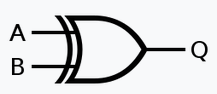
Le XOR joue un rôle fondamental en cryptographie car il possède une propriété très intéressante : \((x\wedge y)\wedge y=x\)
Si \(x\) est un message et \(y\) une clé de chiffrage, alors \(x\wedge y\) est le message chiffré. Mais en refaisant un XOR du message chiffré avec la clé \(y\), on retrouve donc le message \(x\) initial.
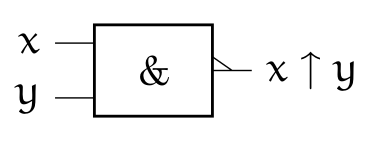
3.2 Fonction Non Et (NAND)⚓︎
x ↑ y = ~(x & y)
Table de vérité de NAND
x |
y |
x ↑ y |
|---|---|---|
| F | F | V |
| F | V | V |
| V | F | V |
| V | V | F |
3.3 Fonction Non Ou (NOR)⚓︎
x ↓ y = ~(x & y)
Table de vérité de NOR
x |
y |
x ↓ y |
|---|---|---|
| F | F | V |
| F | V | F |
| V | F | F |
| V | V | F |
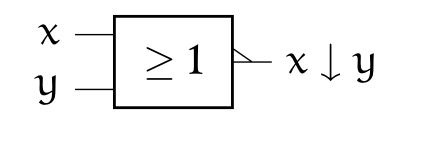
Il est temps de se reposer un peu et d'admirer cette vidéo :
Remarque :⚓︎
Les fonctions NAND ET NOR sont dites universelles : chacune d'entre elles peut générer l'intégralité des autres portes logiques. Il est donc possible de coder toutes les opérations uniquement avec des NAND (ou uniquement avec des NOR).
Exercice 3
Nous allons réutiliser le simulateur de circuits mais en n'utilisant QUE DES PORTES NAND.
Q1. Réaliser la porte AND (avec que des NAND...)
Correction
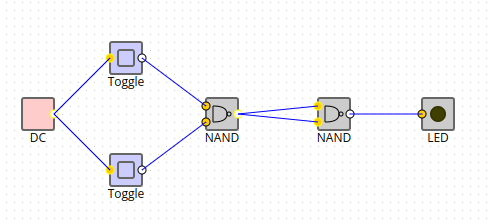
Q2. Réaliser la porte OR (avec que des NAND...)
3.4 Exercice 4⚓︎
Exercice 4
Effectuer les opérations suivantes.
1011011
& 1010101
----------
1011011
| 1010101
----------
1011011
^ 1010101
----------
1011011
&1010101
----------
1010001
1011011
|1010101
----------
1011111
1011011
^1010101
----------
0001110
3.5 Calculs en Python⚓︎
les opérateurs &, | et ^ sont utilisables directement en Python
# calcul A
>>> 12 & 7
4
# calcul B
>>> 12 | 7
15
# calcul C
>>> 12 ^ 5
9
Pour comprendre ces résultats, il faut travailler en binaire. Voici les mêmes calculs :
# calcul A
>>> bin(0b1100 & 0b111)
'0b100'
# calcul B
>>> bin(0b1100 | 0b111)
'0b1111'
# calcul C
>>> bin(0b1100 ^ 0b111)
'0b1011'
Exercice 5 : Cryptographie⚓︎
Exercice 5
On souhaite chiffrer (chiffrer est le mot utilisé en cryptographie pour crypter) le mot "BONJOUR" avec la clé "MAURIAC". Le chiffrement retenu est un chiffrement par XOR, ce qui signifie qu'on va effectuer un XOR entre les deux nombres associés aux lettres.
Exemple :
- la lettre
'B'va être chiffrée grâce au'M'. - Le code ASCII de
'B'est 66. (on le sait carord('B')renvoie 66 ) - Le code ASCII de
'M'est 77. (on le sait carord('M')renvoie 77 ) - 66 ^ 77 vaut 15.
- Le «caractère» associé à 15 est
'\x0f'(on le sait carchr(15)renvoie'\x0f')
Le premier caractère du mot chiffré sera donc '\x0f'
Q1. Écrire une fonction chiffre qui prendra en paramètre un mot mot_clair et un mot de passe cle de même taille que mot_clair et qui renvoie la chaîne de caractères obtenue en XORant mot_clair avec cle.
Correction
1 2 3 4 5 6 | |
Q2. Chiffrer le mot "BONJOUR" avec la clé "MAURIAC".
Correction
>>> chiffre('BONJOUR', 'MAURIAC')
''
Q3. Reprendre la chaîne de caractères précédemment obtenue et la rechiffrer à nouveau avec la clé "MAURIAC". Que constate-t-on ? Etait-ce prévisible ?
Correction
>>> chiffre('', 'MAURIAC')
'BONJOUR'
(a^b)^b = a
Q4. 
Résoudre le Pydéfi La clé endommagée
Correction
1 2 3 4 5 6 7 8 9 10 11 12 13 | |
Complément mathématique: propriétés des opérateurs logiques⚓︎
Les propriétés suivantes sont facilement démontrables à l'aide de tables de vérités: (source : G.Connan)
Toutes ces lois sont aisément compréhensibles si on les transpose en mathématiques :
- & équivaut à \(\times\)
- \(|\) équivaut à \(+\)
- \(\neg\) équivaut à \(-\)